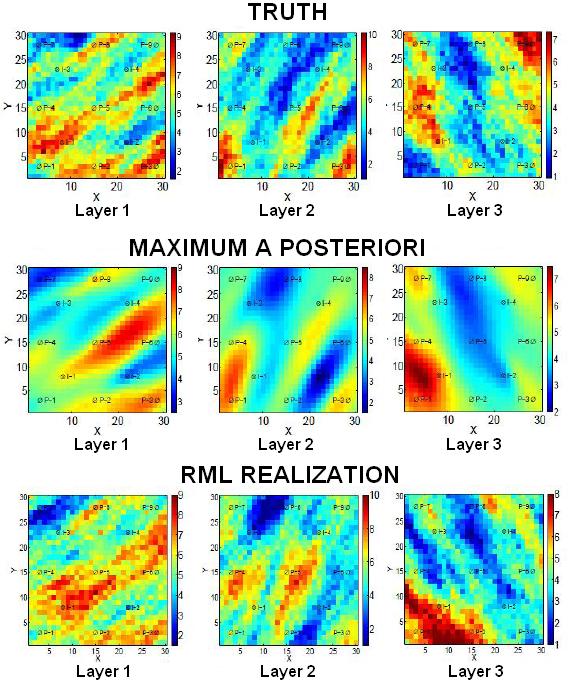
In this research we develop efficient parameterization algorithms for history matching based on the principal right singular vectors of the dimensionless sensitivity matrix corresponding the maximum a posteriori estimate of reservoir model parameter. The necessary singular vectors can be computed with the Lanczos algorithm without explicit computation of the sensitivities. We provide a theoretical argument which indicates that this parameterrization provides an optimal basis for parameterization of the vector of model parameters. We develop and illustrate two gradient-based algorithms based on this parameterization. Like limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm, these algorithms avoid explicit computation of individual sensitivity coefficients. For all synthetic problems that we have considered, the reliability, computational efficiency and robustness of the methods presented here are better than those obtained with quasi-Newton methods.
We also implement the SVD parameterization algorithm to generate a suite of conditional realizations in the randomized maximum likelihood (RML) framework to characterize the uncertainty of reservoir performance predictions. We generate multiple realizations simultaneously by minimizing an ensemble of objective functions concurrently using the singular triplets of a particular realization at each iteration. We show that when combining SVD parameterization with the RML method, we can achieve significant additional computational savings compared to the standard implementation of RML using a quasi-Newton method and this algorithm gives good data matches with history-matched models that are consistent with the prior geology. We present two new algorithms based on this idea, one which relies only on updating the SVD parameterization at each iteration and one which combines an inner iteration based on an adjoint gradient where during the inner iteration the truncated SVD parameterization does not vary. Results with our algorithms are superior to those obtained from the ensemble Kalman filter (EnKF) with and without covariance localization. Finally, we show that by combining EnKF with the SVD-algorithm, we can improve the efficiency of the SVD-algorithms and the reliability of EnKF estimates.