The production optimization step of the “closed-loop” reservoir management is an optimal well control problem determining optimal operating conditions to maximize hydrocarbon extraction or net present value (NPV) for the remaining expected life of a reservoir. It is an important step of the “closed-loop” reservoir management, in which rstly the geological models are calibrated with available data (core, production and seismic data) to reduce the geological uncertainty and secondly a set of optimal well controls are determined based on the new geological models with the production optimization process. Model calibration and production optimization alternate in the “closed-loop” reservoir management process. However, the focus of this study is on production optimization.
The most challenging part of production optimization is to honor the nonlinear constraints or state-control constraints on WOR, GOR, production and injection rates. In this research, we implemented an augmented Lagrangian multiplier method for solving the production optimization problem under linear and nonlinear constraints. Compared to the generalized reduced gradient (GRG) method which is implemented in Eclipse 300, our method does not require the controls to be feasible at every iteration, but the constraints are satisfied within a reasonable tolerance at convergence.
Another challenging problem for production optimization is to solve multi-objective optimization problems, such as long-term and short-term optimization. In the long-term optimization, the primary objective is to determine well controls to maximize either the cumulative oil production or the net present value (NPV) over the expected reservoir life while the short-term optimization refers to maximizing the NPV for the next year or two to ensure suficient cash flow and short-term profit from the upstream production. The long-term and short-term optimization is a complex problem and it involves two objective functions. We proposed to use the augmented Lagrangian method to solve this problem. In addition, as the uncertainty of the oil reservoir is usually modeled by a set of Ne plausible descriptions of the system, we wish to do robust optimization where we maximize expectations of the relevant cost functions.
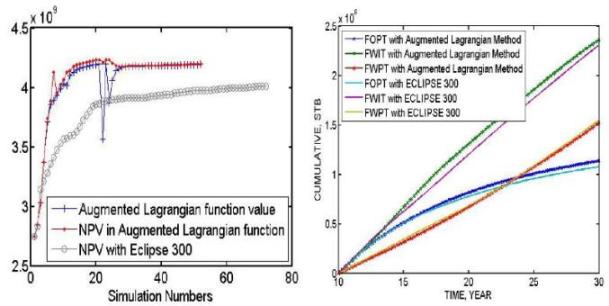
Optimizaiton results for the Brugge field case. Augmented Lagrangian method vs generalized reduced gradient method (Eclipse 300)
Recent publications:
- Zhao, H.; Chen, C.; Do, S.; Oliveira, D.F.B.; Li, G. and Reynolds, A.C.: Maximization of a Dynamic Quadratic Interpolation Model for Production Optimization – accepted for SPE Journal, 2012.
- Chen, C.; Li, G. and Reynolds, A.C.: Robust Constrained Optimization of Short and Long-Term NPV for Closed-Loop Reservoir Management – paper SPE 141314, SPE Reservoir Simulation Symposium, 21-23 February 2011, The Woodlands, Texas, USA.
- Peters, E.; Arts, R.J.; Brouwer, G.K.; Geel, C.R.; Cullick, S.; Lorentzen, R.J.; Chen, Y.; Dunlop; K.N.B.; Vossepoel, F.C.; Xu, R.; Sarma, P.; Alhutali, A.H. and Reynolds, A.C.: Results of the Brugge Benchmark Study for Flooding Optimization and History Matching – SPE Reservoir Evaluation and Engineering, 2011.
- Chen, C.; Wang, Y.; Li, G. and Reynolds, A.C.: Closed-Loop Reservoir Management on The Brugge Test Case, Computational Geosciences, 2010.
- Wang, C.; Li, G. and Reynolds, A.C.: Production Optimization in Closed-loop Reservoir Management, SPE Journal, 2009.